Qって？ HTML5/MathMLを使って

HTML5/MathMLが使えるようになってきてるようなので、せっかくだから使ってみました。

やりかたは、いろいろ調べた結果、

LibreOfficeの数式で書く。
名前を付けて保存(.mmlで)。

それをmiで開く。
＜mathなんたら＞〜＜/math＞の中味を＜math＞〜＜/math＞内にコピペ。

でどうでしょう？
以下、過去記事で実験。MathMLが見られるブラウザ(Safari5.1,FireFox5.01で確認。Chrome12.0.742.122では×）で御覧ください。

で、Q=16ってことは、どのくらいの幅なの？

そもそも、Q=いくらと、なんとかoct.とどういう関係なの？

以下、ひさしぶりに勉強したので忘れないように備忘録。

中心周波数をFc,帯域の下限、上限の周波数をそれぞれF1,F2とすると、Qは

$Q=\frac{F_C}{F_2-F_1}$

  //Qの定義。

帯域幅をW(oct.)とすると

$\begin{array}{c}{F}_2=F_C\ast 2^{W/2}\\ F_1=F_C\ast 2^{-W/2}\\ Q=\frac{F_C}{F_C\ast 2^{W/2}-F_C\ast 2^{-W/2}}\\ \text{=}\frac{1}{2^{W/2}-2^{-W/2}}\end{array}$

//WからQへの変換ができる

$2^{W/2}-2^{-W/2}=\frac{1}{Q}$

$x=2^{W/2}$ , $a=\frac{1}{Q}$ とすると

$x-\frac{1}{x}=a$

$x=\frac{a\pm \sqrt{a^2+4}}{2}$

$x=2^{W/2}>0$なので

$x=\frac{a+\sqrt{a^2+4}}{2}$

$2^{W/2}=\frac{a+\sqrt{a^2+4}}{2}$ //xを元に戻して

$W/2={\log }_2(\frac{a+\sqrt{a^2+4}}{2})$

$W=2{\log }_2(\frac{a+\sqrt{a^2+4}}{2})$

$W=2({\log }_2(a+\sqrt{a^2+4})-1)$

$W=2{\log }_2(a+\sqrt{a^2+4})-2$

$W=2{\log }_2(\frac{1}{Q}+\sqrt{\frac{1}{Q^2}+4})-2$ //aを元に戻す。QからWへの変換ができる。

$W=2\frac{\log (\frac{1}{Q}+\sqrt{\frac{1}{Q^2}+4})}{\log 2}-2$ //底の変換。計算しやすいように。

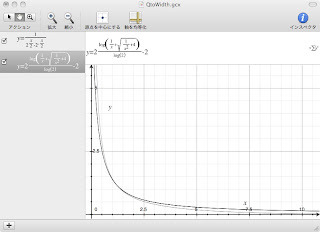
Grapher.appでグラフを書いてみました。

グラフから直読すると、Q=15.9982でW = 0.0902(oct.) ≈ 1/11(oct.)だそうな。

約半音の幅ってことで。

あってます？

以上、過去記事終わり。ふう、疲れた。たくさん書くのはしんどい。

やってみてわかったのだが、このブログだとhtml編集モードでも改行が自動変換されてしまうので、改行を全部消さないといけない。
mi上で全検索して置換（消去）。

あと、やってるうちにLibreOfficeの文法が分かってきた。
Tips:
""でテキスト。
newlineで改行。
"="で行頭のイコール。
" ",{}で表示の微調整。すこし隙間が増える程度。

あんまりきれいにしようとするとMathMLを直接触る羽目に。やめたほうがいい。