Qって？

で、Q=16ってことは、どのくらいの幅なの？
そもそも、Q=いくらと、なんとかoct.とどういう関係なの？
以下、ひさしぶりに勉強したので忘れないように備忘録。

中心周波数をFc,帯域の下限、上限の周波数をそれぞれF1,F2とすると、Qは
Q=Fc/(F2-F1) //Qの定義。

帯域幅をW(oct.)とすると
F2=Fc*2^(W/2) , F1=Fc*2^(-W/2)
Q=Fc/(Fc*2^(W/2)-Fc*2^(-W/2)
=1/(2^(W/2)-2^(-W/2)) //WからQへの変換ができる

2^(W/2)-2^(-W/2)=1/Q
x=2^(W/2) , a=1/Qとすると
x-1/x=a
x^2-ax-1=0
x=(a±sqrt(a^2+4))/2
x=2^(W/2)>0なので
x=(a+sqrt(a^2+4))/2
2^(W/2)=(a+sqrt(a^2+4))/2 //xを元に戻して
W/2=log2((a+sqrt(a^2+4))/2)
W=2*log2((a+sqrt(a^2+4))/2)
=2*(log2(a+sqrt(a^2+4))-1)
=2*log2(a+sqrt(a^2+4))-2
=2*log2(1/Q+sqrt(1/Q^2+4))-2 //aを元に戻す。QからWへの変換ができる。
=2*log(1/Q+sqrt(1/Q^2+4))/log(2)-2 //底の変換。計算しやすいように。

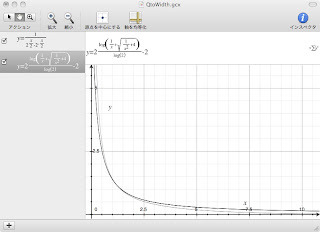
Grapher.appでグラフを書いてみました。

グラフから直読すると、Q=15.9982でW = 0.0902(oct.) ≈ 1/11(oct.)だそうな。
約半音の幅ってことで。
あってます？